A Derivation of the Bose–Einstein distribution
Suppose we have a number of energy levels, labelled by index i, each level having energy εi and containing a total of ni particles. Suppose each level contains gi distinct sublevels, all of which have the same energy, and which are distinguishable. For example, two particles may have different momenta, in which case they are distinguishable from each other, yet they can still have the same energy. The value of gi associated with level i is called the "degeneracy" of that energy level. Any number of bosons can occupy the same sublevel.
Let w(n,g) be the number of ways of distributing n particles among the g sublevels of an energy level. There is only one way of distributing n particles with one sublevel, therefore w(n,1) = 1. It's easy to see that there are n + 1 ways of distributing n particles in two sublevels which we will write as:
With a little thought it can be seen that the number of ways of distributing n particles in three sublevels is w(n,3) = w(n,2) + w(n−1,2) + ... + w(0,2) so that
where we have used the following theorem involving binomial coefficients:
Continuing this process, we can see that w(n,g) is just a binomial coefficient
The number of ways that a set of occupation numbers ni can be realized is the product of the ways that each individual energy level can be populated:
where the approximation assumes that gi > > 1. Following the same procedure used in deriving the Maxwell–Boltzmann statistics, we wish to find the set of ni for which W is maximised, subject to the constraint that there be a fixed number of particles, and a fixed energy. The maxima of W and ln(W) occur at the value of Ni and, since it is easier to accomplish mathematically, we will maximise the latter function instead. We constrain our solution using Lagrange multipliers forming the function:
Using the gi > > 1 approximation and using Stirling's approximation for the factorials  gives:
gives:
Taking the derivative with respect to ni, and setting the result to zero and solving for ni yields the Bose–Einstein population numbers:
It can be shown thermodynamically that β = 1/kT where k is Boltzmann's constant and T is the temperature, and that α = -μ/kT where μ is the chemical potential, so that finally:
Note that the above formula is sometimes written:
where z = exp(μ / kT) is the absolute activity.

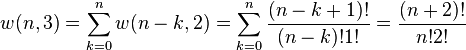






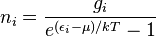
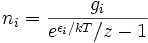

1 comment:
too good!
Post a Comment